طراحی و توسعه بازیهای دیجیتال میتواند یک فعالیت پیچیده باشد که متخصصان رشتههای مختلف را درگیر کند. در این مقاله، که در سال 2019 در نشریه معتبر Games &Cultures به انتشار رسیده است،از نظریه بازیها[1] برای طراحی گیم پلی یک بازی دیجیتال استفاده شده است و این مطلب به شکل کاربردی در درختان تصمیمگیری و ماتریسهای تاوان نشان داده میشود. این مقاله را پژوهشگر همکار دایرک، سرکار خانم ریحانه رفیعزاده اخویان، دانشجوی دکتری پژوهش هنر دانشگاه الزهرا بررسی کردهاند.
مقدمه
بازیهای دیجیتال مدرن ممکن است از صدها هزار یا حتی میلیونها خط کد برنامهنویسی تشکیل شده باشند. بهطورمعمول، بازیهای دیجیتال مدرن شامل انواع ورودیهای گسسته و پیوسته (دیجیتال و آنالوگ) از بازیکن هستند که یک سیستم چندرسانهای غنی و پیچیده را کنترل میکنند. درواقع هیچ مدل واحدی بهعنوان بهترین مدل برای توسعه بازیهای دیجیتال وجود ندارد و برای هر بازی تصمیمگیریهای خاص خود آن بازی موردنیاز است. آنچه در این مقاله بررسی میشود این است که چگونه میتوان نظریه بازی را برای طراحی بازیهای دیجیتال استفاده کرد. بهطور خاص، بررسی میشود که چگونه میتوان از نظریه بازی برای ایجاد درختان تصمیمگیری[2] در سطح بالا استفاده کرد؛ این درختان بهصورت تصویری مسیرهای اصلی گیم پلی را نمایش میدهند و بازنماییهای نمادین اشیاء بازی شامل اشیاء ثابت، قابلحمل و تعاملی را -در بخشی از یک بازی رایانهای-شامل میشوند. علاوه بر این، این مطلب نیز که چگونه میتوان از ماتریسهای تاوان[3] برای طراحی سطوح مهارت و چالش بخشهای مختلف یک بازی دیجیتال استفاده کرد بررسی میشود.
دلیل منطقی استفاده از نظریه بازی در طراحی بازیهای دیجیتال-و بهویژه برای ایجاد تکنیکهایی برای نمایش گیم پلی مبتنی بر نظریه بازی-این است که مدلسازی، توصیف و مستندسازی گیم پلی واقعی در یک بازی دیجیتال میتواند دشوار باشد. استفاده از این نظریه برای شناسایی، الگوسازی، مستندسازی و ایجاد ارتباط میان انتخابهای (تصمیمگیری) اصلی بازیکن و تعاملاتی که باعث تغییر در گیم پلی- بر اساس ورودیهای بازیکن و سطح مهارت یا چالشهای بخشهای مختلف بازیهای دیجیتال– میشود مفید خواهد بود. نظریه بازی مکانیسمی بصری را برای بررسی آنچه در هنگام انجام بازی در یک رایانه اتفاق میافتد فراهم میکند. اگرچه درختان تصمیمگیری دقیق ریاضی میتوانند حتی برای سادهترین بازیهای دیجیتال کاملاً پیچیده و ناخوشایند باشند، اما میتوان آنها را برای نمایش سطح بالاتر مسیرهای بازی سازگار کرد و با ترکیب بازنمود نمادین عناصر بازیها، آنها میتوانند به شکلی بصری و ساده و آسان نحوه گیم پلی در بخشی از بازی دیجیتال را نمایش دهند. علاوه براین میتوان از ماتریسهای تاوان برای پشتیبانی از طراحی سطح مهارت و چالش بخشهای مختلف یک بازی دیجیتال استفاده کرد.
ادبیات تحقیق
نظریه بازی در ابتدا بهعنوان شاخهای از اقتصاد توسعه یافت. این نظریه مربوط به مطالعه ریاضیوار تصمیمگیری است و برای مدلسازی نحوه رفتار افراد در شرایط خاص که شبیه انواع ساده بازیها است ایجاد شده است. از نظریه بازی میتوان برای بررسی روابط بین تصمیمات و نتایج استفاده کرد. یک بازی در چهارچوب نظریه بازی میتواند بهعنوان یک مسابقه (بازی) میان حریفان (بازیکنان) که تحت محدودیت (قواعد) برای یک هدف فعالیت میکنند توصیف شود. از نظریه بازی میتوان برای ساختاربندی و تحلیل موقعیتهای مشکل استفاده کرد. الگوسازی صوری از وضعیت بهعنوان یک بازی میتواند شامل تعیین بازیکنان و گزینههای آنها و در نظر گرفتن استراتژیها و ترجیحات باشد.
نظریه بازی شامل مفهوم سود[4] است که میتواند بهعنوان یک معیار ریاضی برای رضایت بازیکن توصیف شود. در نظریه بازی، برای کلیه نتایجی که یک تصمیم ممکن است داشته باشد، سودی را میتوان به آن تصمیم اختصاص داد. مفهوم دیگر در نظریه بازی، ویژگی نقطه زینی[5] است که مربوط به انتخابهایی از بازیکنان بازی است که منجر به نتیجه یکسان میشوند. مفهوم دیگر نظریه بازی ماتریس تاوان است که فرایند تصمیمگیری را به ساختار شبکه مانند ترسیم میکند. یک محور شبکه نمایانگر تصمیم یک بازیکن و محور دیگر شبکه نشاندهنده تصمیم بازیکن دیگر است. سلولهای درون شبکه، نتایج ناشی از تصمیمهای گرفتهشده را نشان میدهند.
رویکردهای طراحی بازی کامپیوتری
رویکردهای مختلفی برای طراحی بازیهای دیجیتال توسعهیافته است که شامل فلوچارتها، استوری بورد، نقشهها یا نمودارهای توپولوژیکی (با داشتن گرههایی که صحنهها را نشان میدهند و اضلاعی که نمایانگر گذار بین آنهاست)، مدلهای انتقال حالت و زبان مدلسازی یکپارچه (UML) میشود. با توجه به آنچه گفته میشود میتوان برای طراحی گیم پلی از درختان تصمیمگیری استفاده کرد. شاخههای مختلف در درخت تصمیمگیری مربوط به مسیرهای مختلفی است که کاربر انتخاب میکند یا نتیجه کنش بازیکن است. درواقع یک درخت تصمیمگیری، نمودار شاخهای درختی است که میتواند مجموعه اقدامات و تصمیمات احتمالی را که یک بازیکن میتواند در یک بازی اتخاذ کند تشریح کند. درختان تصمیمگیری میتوانند نحوه حرکت بازیکنان را در فضای احتمالات بازی دیجیتال مدلسازی کنند. در تشریح صحبت از طراحی بازی محققان به تعریف چهارچوب مکانیک- دینامیک – زیباییشناسی پرداختهاند: مکانیک بازی اجزای خاص بازی را در سطح نمایش دادهها و الگوریتمها توصیف میکند؛ دینامیک بازی رفتار زمان اجرای مکانیک بازی را که با ورودیهای بازیکن و دیگر عوامل درگذر زمان در ارتباط است توصیف میکند و زیباییشناسی مربوط به پاسخهای عاطفی برانگیختهشده در بازیکن است.
نظریه بازی برای طراحی بازی کامپیوتری
نظریه بازی روابط بین تصمیمات و نتایج را بررسی میکند. تعامل بین کنشها و نتایج میتواند برای مدلسازی گیم پلی استفاده شود. دیدن یک طراحی بازی دیجیتال از منظر نظریه بازی شامل مشاهده یک بازی دیجیتال بهعنوان یک سری از تصمیمات استراتژیک است که توسط بازیکن گرفته میشود. گیم پلی درون یک بازی دیجیتال را میتوان با قوانین نظم و ساختار داد. قوانین میتوانند شکل درونی یا سازماندهی یک بازی دیجیتال را تشکیل دهند و شاکلههای قانونی میتوانند ابزارهای تحلیلی را ارائه دهند که بهصورت ریاضیوار بازیهای دیجیتال را تشریح میکنند. از نظریه بازی میتوان برای توسعه قوانین بازی برای یک بازی دیجیتال استفاده کرد. درختان تصمیمگیری که میتوانند بهصورت صوری و ریاضیوار مسیرهای درون یک بازی دیجیتال را نشان دهند، میتوانند به طراحان بازیهای دیجیتال برای درک این مطلب که چگونه بازیکنان بازی میتوانند از طریق فضای احتمالات و امکانات در قسمتهای مختلف یک بازی دیجیتال حرکت کنند کمک کنند.
نتایج تحقیق
نظریه بازی برای طراحی بازی کامپیوتری
حتی برای یک بازی ساده نظیر بازی دوز درخت بازی یک تصویر پیچیده و بدریخت خواهد بود. با توجه به تعداد حرکتهای ممکن تعداد شاخهها در این درخت فاکتوریل عدد 9 یعنی 9*8*7*6*5*4*3*2*1 خواهد بود. البته میتوان پیچیدگی این درخت را با استفاده از محدودیتهایی کاهش داد؛ بهعنوانمثال درحرکت اول به دلیل تقارن و تساوی در فضای حرکت، اینکه کاربر کدامیک از چهارگوشه را انتخاب کند تفاوتی ایجاد نمیکند. همین مسئله دربازیهای مهاجم اولشخص هم دیده میشود چراکه بهعنوانمثال با داشتن انتخاب برای تعویض میان دو اسلحه گیم پلی بازی فرقی نخواهد کرد. البته ازنظر ظاهری ممکن است انتخاب سلاحها ایجاد تفاوت کند اما در تعامل با دیگر اشیای بازی نتیجه یکسان خواهد بود.
درخت تصمیمگیری برای طراحی بازیهای رایانهای
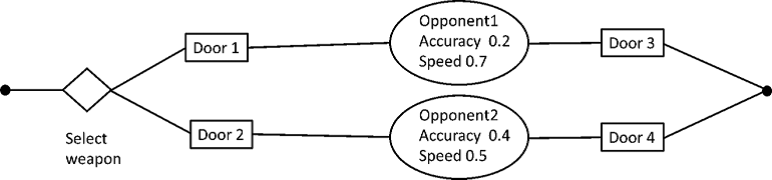
در اعمال نظریه بازی در طراحی بازیهای دیجیتال، هنگام ایجاد درختان تصمیمگیری (درختهای بازی)، تعاملات بازی (نقاط اصلی تصمیمگیری) از همه مهمتر است. تعاملات بازی میتواند با اشیاء بیجان ثابت (که میتوانند در یک درخت تصمیم با جعبهها نمایان شوند) یا با اشیاء متحرک (که میتوانند بهصورت گرافیکی در داخل یک درخت تصمیم توسط بیضیها نمایان شوند) یا اشیاء بازی قابلحمل[6] (که میتواند توسط یک لوزی در یک درخت تصمیمگیری نمایان شود) باشد. از درختان تصمیمگیری میتوان برای تعیین احتمال وقوع حوادث استفاده کرد؛ مثلاً برای تخمین احتمال شیر یا خط در بازی پرتاب سکه؛ اما دربازیهای پیچیده دیجیتال، محاسبه احتمال موفقیت (تکمیل یک بخش بازی خاص) به روش درخت تصمیمگیری ریاضی صوری مشکل است. باوجوداین، میتوان احتمال موفقیت را با توجه به پارامترهای موردنیاز برای موفقیت نشان داد. بهطورمعمول، در اکثر بازیهای دیجیتال، با استفاده از مجموعه کنترلی ارائهشده توسط کنترلگر بازی، اصلیترین پارامترهای اعمالشده توسط بازیکن بازی، انتخاب (کدام دکمه را فشار دهد)، سرعت (دکمه چقدر سریع فشرده شود یا دسته بازی قدر سریع حرکت کند) و دقت (با چه دقتی دسته بازی در جهت یا جهات خاص حرکت کند) هستند.
محدودیت عمده درختان تصمیمگیری ریاضی صوری، ماهیت ساختاری آنها ازنظر ترتیب تصمیمات است. بهغیراز حالتی که یک بازی دیجیتال به شکلی دقیق و با نظمی معین انجام شود، تلاش برای ایجاد یک درخت تصمیم برای کل یک بازی نامناسب خواهد بود. بااینحال در مقیاس کوچکتر یعنی در بخشهایی از بازی یا بخشهای مأموریت، درختان تصمیمگیری میتوانند چهارچوبی مفید برای طراحی گیم پلی ارائه دهند.
هر شاخه در درخت تصمیم مجموعهای از حالتهای بازی (بهعنوانمثال، میزان مهمات و وضعیت سلامتی در یک بازی تیرانداز اولشخص) و مجموعهای از ورودیهای بازی (بهعنوانمثال، سرعت و جهت حرکت به سمت یک هدف بازی) را نشان میدهد. پیچیدگی و اندازه درخت تصمیمگیری برای طراحی بازی در یک بخش خاص، میتواند به یکمیزان قابلکنترل از اندازه و پیچیدگی کاهش یابد.
مفهوم سود در نظریه بازیها
مفهوم سود در نظریه بازی (که میتواند بهعنوان یک اندازهگیری ریاضی از رضایت بازیکن توصیف شود) میتواند با در نظر گرفتن رضایت بازیکن در رابطه با بازیها در طراحی بازیهای دیجیتال گنجانده شود. در این بازیها تنوع زیادی از گزینهها (همانطور که در مسیرهای مختلف درون ساختارهای تصمیمگیری درختی نشان دادهشده است) و سطح مناسبی از چالش (همانطور که توسط عواملی مانند سرعت و دقت ورودیهای بازیکن نشان داده میشود) بهمنظور تکمیل بخشهای مختلف بازی دیجیتال وجود دارد.
مفهوم نقطه زین دربازیها
مفهوم نقطه زینی در نظریه بازی در مورد انتخابهایی از بازیکنان بازی است که به نتیجه یکسان منجر میشود. یک نقطه زینی را میتوان بهعنوان یکراه حل بهینه برای یک بازی دیجیتال مشاهده کرد. بهعنوانمثال، اگر در یک بازی مهاجم اولشخص، انتخاب نوع خاصی از سلاح (بهعنوانمثال مسلسل) به این معنی است که بازیکن تقریباً همیشه بهراحتی آن بخش خاص از بازی را تکمیل میکند، پس ممکن است بازیکن همیشه آن انتخاب را داشته باشد که درنتیجه معنا و تنوع گیم پلی کمتر میشود. ساخت دقیق درخت تصمیمگیری میتواند از ایجاد نقاط زین (مسیرهای میانبر ساده) برای بازیکن در طراحی بازی دیجیتال جلوگیری کند.
ماتریس تاوان دربازیها
تعادل در بازی شامل سه دسته مختلف میشود:
- تعادل بازیکن – بازیکن: منصفانه بودن دربازیهای چندنفره بهطوریکه هر بازیکن بهغیراز مهارت خود مزیتی ندارد.
- تعادل بازیکن-گیم پلی: تضمین انطباق منحنی یادگیری بازیکن با پاداشهایی که دریافت میکند.
- تعادل گیم پلی – گیم پلی: ویژگیهای درون بازی با یکدیگر متعادل میشوند.
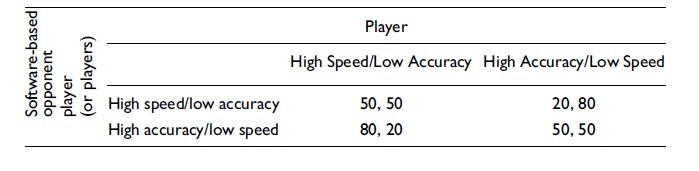
مفهوم ماتریس تاوان میتواند برای مدلسازی فرایند تصمیمگیری بازیکن در یک ساختار شبکه مانند بهمنظور تجزیهوتحلیل، مستندسازی و برقراری ارتباط میان سطح مهارت یا چالش در بخشهای بازی دیجیتال استفاده شود. یک ماتریس تاوان را میتوان بهعنوان یک نمایش تصویری از کلیه نتایج احتمالی که میتواند رخ دهد- هنگامیکه دو فرد مجبور به تصمیمگیری استراتژیک هستند- توصیف کرد. یک محور ماتریس تاوان میتواند تصمیم بازیکن را نشان دهد. محور دیگر ماتریس تاوان میتواند بازیکن حریف (مبتنی بر نرمافزار) باشد. سلولهای موجود در ماتریس تاوان، نتایج ناشی از تصمیمات بازیکن و حریف (مبتنی بر نرمافزار) را نشان میدهند. برای بازیهای ساده مانند بازیهایی که بازیکن یک گزینه را از بین طیفهای مختلف انتخاب میکند، ماتریس تاوان میتواند بسیار ساده باشد. همانطور که در درختان تصمیمگیری برای طراحی بازیهای دیجیتال نشان داده شد، استفاده از ماتریس برای هر تصمیم و اقدام احتمالی که توسط یک بازیکن بازی دیجیتال دربازیهای پیچیدهتر انجام میشود ناخوشایند و غیرممکن خواهد بود. باوجوداین، استفاده از ماتریسهای تاوان در سطح بالا که الگوی تصمیمگیریهای سطح عمومیتر را نشان میدهند عملی است. بهعنوانمثال دریکی از اولین بازیهای دیجیتال به نام پونگ (یک بازی شبیهسازی تنیس روی میز)، دقت حرکات انجامشده توسط بازیکن روی نتیجه بازی تأثیر میگذاشت، زیرا تماس توپ با لبههای بیرونی دسته پینگپنگ بازگشت توپ در زاویههای کوچکتر (و دشوارتر) را همراه داشت؛ بنابراین، یک ماتریس تاوان برای این بازی دیجیتال میتواند نتایج دقت بالا و پایین بازیکن را بهعنوان تصمیمات عمومی مدلسازی کند. حتی وقتی ماتریسهای تاوان فقط یک الگوی بسیار انتزاعی از یک بازی هستند، میتوانند در تعادل بخشیدن به عناصر مختلف طراحی بازی مفید باشند.
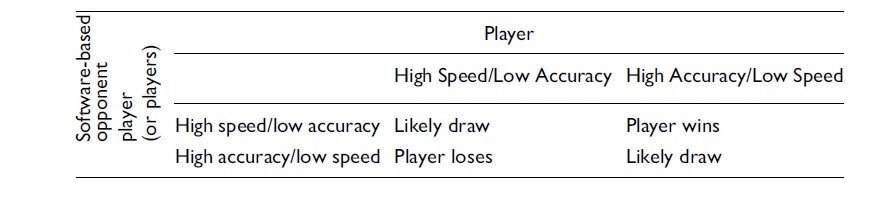
عناصر ماتریس تاوان را میتوان توسط طراح بازی دیجیتال تخمین زد و یا میتوان با انجام آزمایشهایی با بازیکنان واقعی در یک محیط آزمایش برای تعیین توزیع نتایج، ازنظر آماری تعیین کرد. این آزمایش درواقع میتواند احتمال موفقیت بازیکنان بازی را هنگام شرکت در گیم پلی بخشهای مختلف بازی دیجیتال بررسی کند. تست کردن بازی کاری است که یک طراح بازیهای دیجیتال میتواند در کل مراحل طراحی یک بازی دیجیتال انجام دهد تا بتواند بینشی در مورد این موضوع داشته باشد که بازی دیجیتال در حال دستیابی به اهداف موردنظر خود در تجربه بازیکن است یا نه. برای بازیهای دیجیتال چندنفره آنلاین، میتوان از تجزیهوتحلیل آماری استراتژیهای استفادهشده توسط تعداد زیادی از بازیکنان استفاده کرد که این کار میتواند برای طراحی بازی مفید باشد. بهطور خلاصه، ماتریسهای تاوان در ابتدا ممکن است توسط یک طراح بازی ارائه شود که متغیرها در برابر نتایج اندازهگیری میشود و تخمینهای اولیه صورت میگیرد؛ اما برای دستیابی به تجربه مناسب گیم پلی برای انواع بازیکنان بازی، انجام آزمایشها برحسب متغیرهای درگیر صورت میگیرد تا اطمینان حاصل شود که ماتریسهای تاوان نمایانگر آماری گیم پلی هستند.
نتیجهگیری
در این مقاله، نشان داده شد که چگونه میتوان مفاهیم نظریه بازی را در طراحی بازیهای دیجیتال برای طراحی مسیرهای گیم پلی، دشواری مراحل و اشکال پیشرفتهتر گیم پلی به کار برد. نظریه بازی میتواند یک روش صوری را برای درک تصمیمگیری در یک محیط بازی دیجیتال ارائه دهد و در طراحی بازی دیجیتال مفید باشد. بهمنظور طراحی بازیهای دیجیتال که سطح مناسبی از چالش و تنوع در انتخابها و مسیرهای گیم پلی را ارائه میدهند، میتوان از نظریه بازی برای کمک به طراحی ساختار کلی گیم پلی استفاده کرد. یک بازی ساده مثل دوز میتواند انواع مسیرهایی را نشان دهد که یک بازی ساده دیجیتال نیز میتواند شامل آن شود. نظریه بازی را میتوان با استفاده از ساختارهای درختی تصمیمگیری سطح بالا برای ترسیم مسیرهای اصلی بازی، نقاط تصمیمگیری اصلی و با در نظر گرفتن رابطه کنش بازیکن با احتمال موفقیت در یک بخش از بازی، به شیوهای عملی و قابلاستفاده به کار برد.
منبع
Taylor, M. Baskett, M. Reilly, D. & Ravindran, S. (2019). Game theory for computer games design. Games and Culture, 14(7-8), 843-855.
[1] Game Theory
[2] decision trees
[3] payoff matrices
[4] utility
[5] saddle point
[6] portable